TYPOLOGY OF OUR EDUCATIONAL MODELS

3. Construct

3.1. Compass-and-Ruler Constructions

One of the largest and most important classes of 1C:MathKit activities comprised of geometric construction problems. Any classical compass-and-ruler construction problem or a problem with a different set of drawing tools can be shaped into an interactive activity. A special feature of a dynamic construction is that it can be tested by varying its initial data both when it's finished or at any intermediate step. It may happen, for instance, that drawing a line through a previously constructed point, you hit a point that is very close, but not exactly the desired one. Such a drawing will seem to be correct, but it will fall apart as its initial objects are dragged. Data variation is also useful in experimental analysis of the number of solutions to the problem and their existence. In addition, construction activities can be supplied with automatic answer checking, as in the following model.

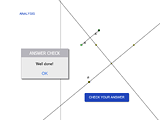Reflecting a Point

3.2. Custom Toolbar

Another interesting feature of 1C:MathKit is the customizable toolbar. Firstly, the author can leave in the model only the tools that are actually needed in the given problem, considerably simplifying its interface. Secondly, the author can assign different sets of tools to the same problem, and this can dramatically change the idea of the solution, the required set of concepts and facts. Thus the same problem gives rise to a variety of activities. For example, a very simple problem 3.1 becomes much more interesting if we try to solve it with a straightedge alone.

Reflecting a Point by Straightedge Alone

3.3. 3D Constructions

Next is an example of a three-dimensional activity, in which students are to make a construction on a given rotating model of a solid. In fact, the same problem can be posed for an ordinary drawing and ordinary tools; not only that, the construction steps will basically be the same in both cases. What makes a great difference is the hidden rotating frame to which the solid in the drawing is attached. So in the course of construction students can choose the most convenient view of the figure which allows them to understand better the positional relationships of its elements, and, in general, to improve their spatial imagination. In a way, this kind of activities takes place between two and three dimensions.

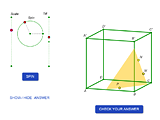Cutting the Cube

3.4. Transforming Function Graphs

Constructive activities involving function graphs do not boil down to plotting functions of one variable, i.e., graphs of equations y = f(x). It is possible to construct parametric curves, graphs of equations of the form F(x, y) = 0, tangents to curves, regions bounded by curves, etc. Much attention in the school course is given to construction of graphs by transformations, where the graph in question is obtained from a certain standard one by translations, dilations along axes, and reflections. MathKit has special tools for these transformations, and the next activity is based on these tools.

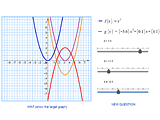Transforming Parabolas

Previous page	TYPOLOGY OF EDUCATIONAL MODELS	Next page