1С:Виртуальная лаборатория

Отрезки BM, b и c – произвольные, в чем легко убедиться, перемещая точки на чертеже. Соответственно, и построение, служащее решением задачи, должно сохранять свою правильность при различных длинах отрезков.

Неправильное построение

1

Попробуем решить задачу «в лоб». Вершины А и C искомого треугольника находятся, соответственно, на расстоянии b и c от точки B. Построим окружности с соответствующими радиусами и центром в точке B.

Для этого на панели инструментов выберем инструмент «Построить окружность по центру и отрезку-радиусу».

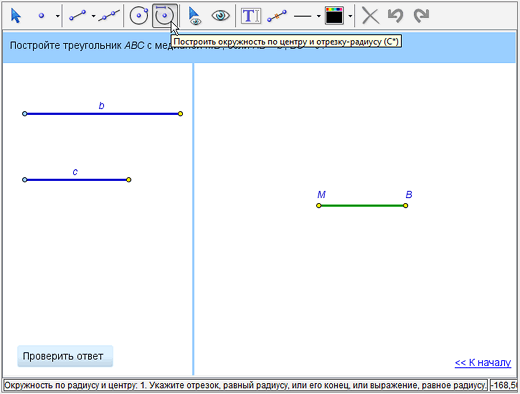
Обратите внимание на вид курсора, появляющегося после выбора инструмента, и подсказку в статусной строке внизу – они напоминают правильную последовательность действий при построении:

сначала нужно отметить отрезок-радиус (отрезки b и c) или указать его концы (точки, являющиеся концами соответсвующих отрезков),

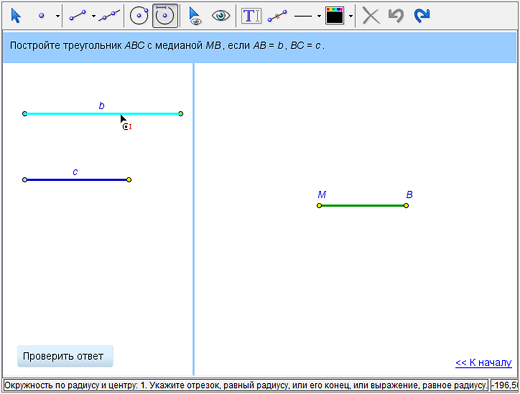
а затем отметить центр откужности (точку B).

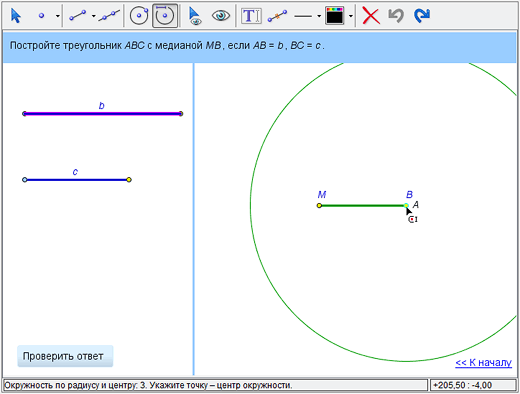
2

Поставим на окружность радиуса b точку A (в данном случае это большая окружность, если не менять исходные длины отрезков). Для этого выберем инструмент «Точка», подведем курсор к окружности, пока она не «подсветится», и поставим точку.

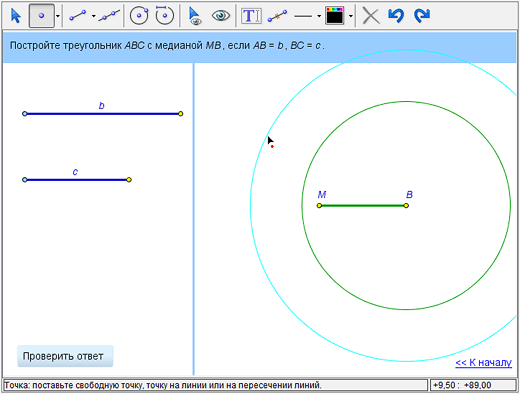
В данном случае получившаяся точка автоматически будет обозначена буквой A. Чтобы изменить обозначение точки, нужно щелкнуть мышкой по обозначению или выбрать инструмент «Создать обозначение или текстовое поле» и применить его к точке.В появившемся текстовом поле нужно написать новое обозначение и нажать Enter. Если получившееся обозначение расположилось неудачно, вы можете переместить его на другое место в окрестности подписанного объекта. Для этого выберите инструмент выбора и премещения (стрелка) и подвиньте обозначение.

3

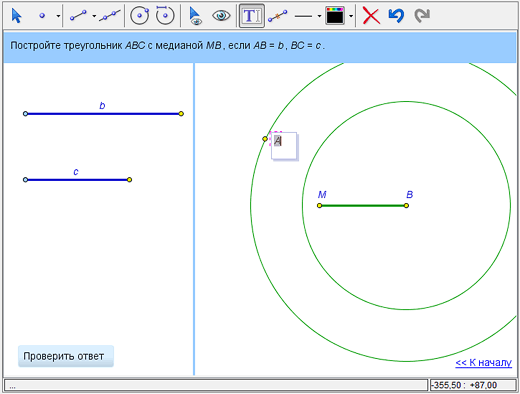
Построим точку С. Из условий задачи известно, что точка M лежит на середине отрезка AC. Построим прямую АM, поочередно щелкнув в точки А и М соответствующим инструментом.

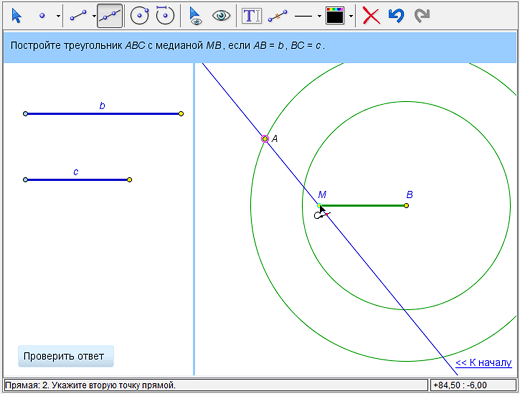
При помощи инструмента «Построить окружность по центру и точке на ней» построим окружность с центром в точке М и радиусом МА.

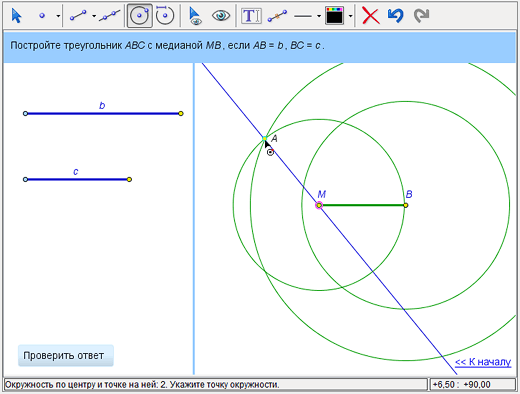
Очевидно, что точка С лежит на пересечении этой окружности с прямой АМ. При помощи инструмента «Создать точку» поставим точку С на пересечении линий (обе они должны подсветиться одновременно при установке курсора на их пересечение).

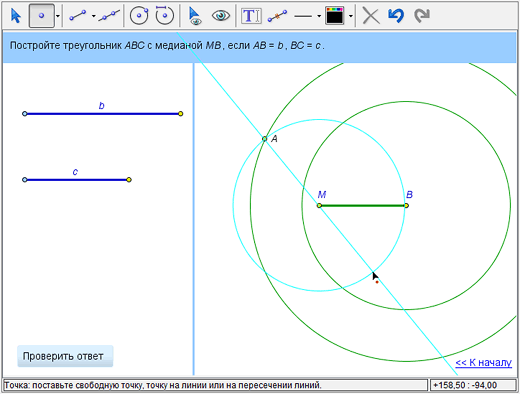
4

При помощи инструмента «Построить отрезок» строим стороны АВ и СВ.

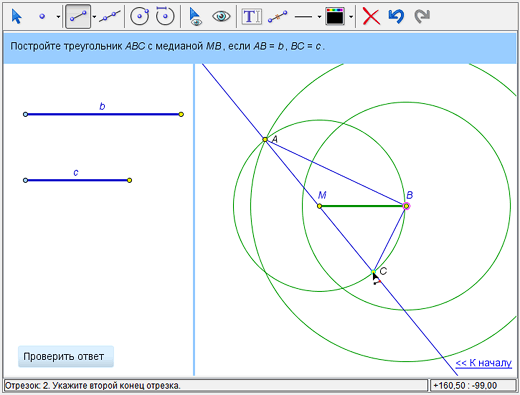
Что не так? Выполнены не все условия задачи: ВМ действительно является медианой треугольника АВС, но длина стороны СВ не равна с. Сейчас «исправим»: сдвинем точку А так, чтобы точка С попала на окружность с центром В и радиусом с. Готово? Узнаем, нажав кнопку «Проверить ответ».

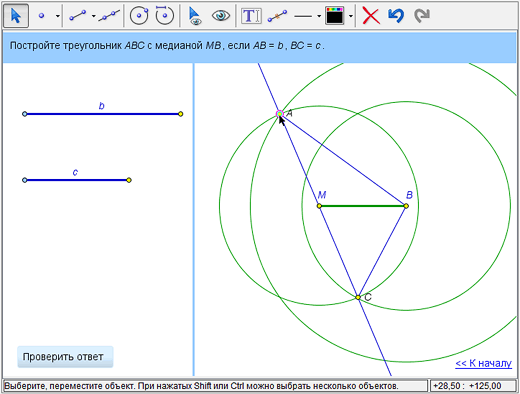
Наше построение ошибочно, так как все искомые точки должны быть построены (циркулем и линейкой), а не найдены «на глазок». И наш чертеж сам подскажет, что он получен рисованием, а не строгим построением. Измените длину любого изначально заданного отрезка – и точка С «сползет» с окружности, ведь она оказалась на ней не в результате точного построения, а лишь при визуальной «подгонке».

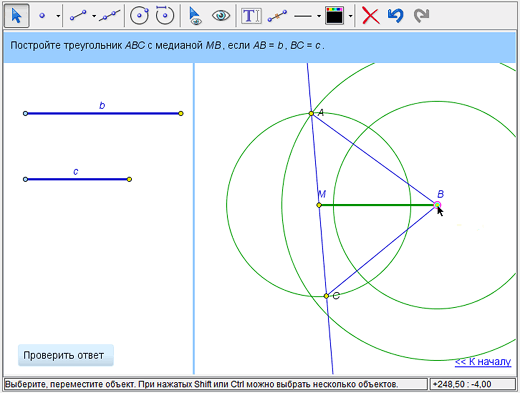
Мы должны были точно определить положение точки А на окружности с радиусом b, а не ставить ее произвольно. Как же это сделать?

5

Нажмем ссылку «К началу» – она вернет наш чертеж в исходное состояние.

Правильное построение

1

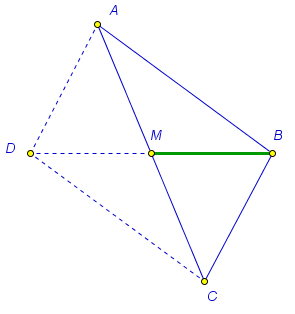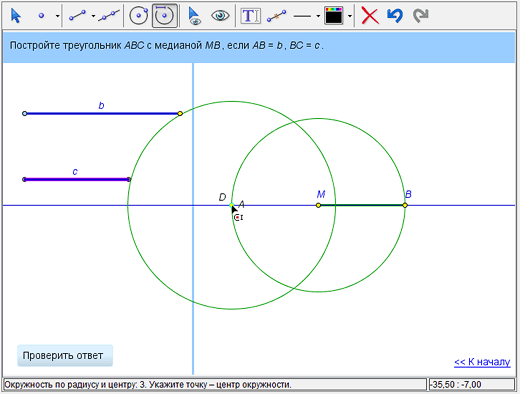
Прежде чем начать строить, следует придумать способ построения. В данной задаче удобно воспользоваться теоремой о том, что диагонали параллелограмма делятся точкой их пересечения пополам.

Мысленно достроим искомый треугольник АВС до параллелограмма АВСD. Поскольку сторона АС треугольника является диагональю параллелограмма, а точка M – ее середина, вторая диагональ ВD будет вдвое длиннее отрезка ВМ. Это позволяет построить точку D. Проведем прямую BM, потом построим окружность с центром в точке М и радиусом МВ. На продолжении отрезка BM за точку M отметим точку пересечения с окружностью. Это и будет точка D.

2

Поскольку противоположные стороны параллелограмма равны, то расстояние от D до А равно длине c стороны BC. Значит, А лежит на пересечении двух окружностей – окружности с центром В и радиусом b и окружности с центром D и радиусом с. Если эти окружности пересекаются, то одну из точек пересечения и возьмем в качестве точки А.

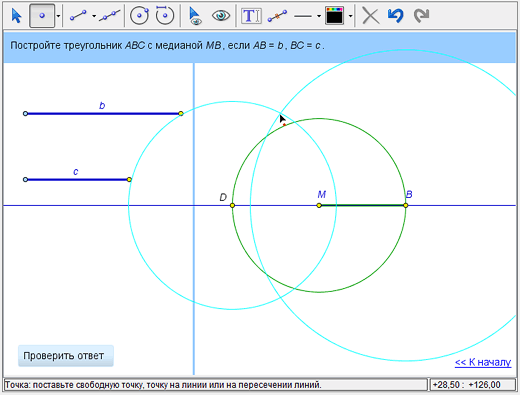
3

Точку С можно теперь легко построить разными способами. Можно, аналогично построению точки А, найти точку пересечения окружностей – окружности с центром в точке В и радиусом с и окружности с центром в точке D и радиусом b. Можно, по аналогии с построением точки D, найти пересечение прямой АМ и окружности с центром в точке М и радиусом МА.

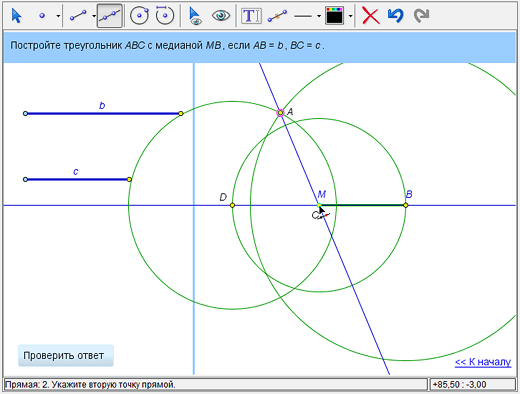
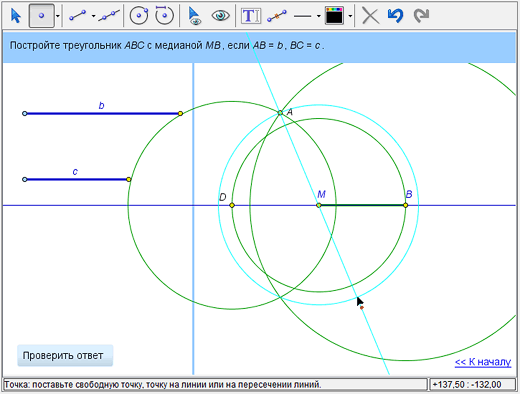
4

При помощи инструмента «Построить отрезок» строим стороны АВ и СВ.

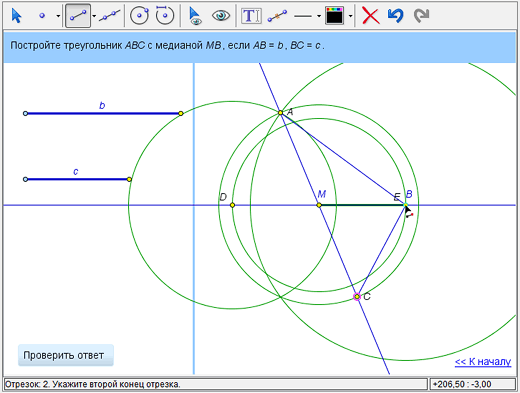
Проверяем построение, нажав кнопку проверки. Ошибка! Почему? Потому что программа считает треугольник построенным, если, как это и должно быть, построены все его стороны. А мы ещё не соединили отрезком вершины А и С. При помощи инструмента «Построить отрезок» строим отрезок АС, поочередно щелкая курсором по соответствующим точкам. Проверяем построение: построение верное!

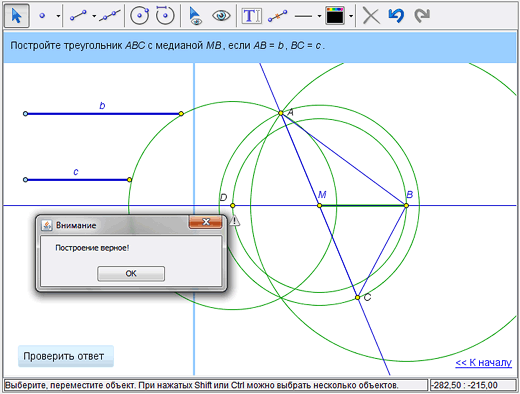
5

Теперь можно улучшить оформление чертежа. Во-первых, можно выделить искомые отрезки АВ, ВС и СА. Сначала, воспользовавшись инструментом «Стиль линии», сделаем линии отрезков потолще. (Обратите внимание: когда вы применяете инструмент к наложенным друг на друга объектам, выпадает меню, в котором можно выбрать нужный вам объект из списка – в нашем случае отрезок АС, а не прямую.) Затем покрасим отрезки, например в красный цвет, при помощи инструмента «Цвет».

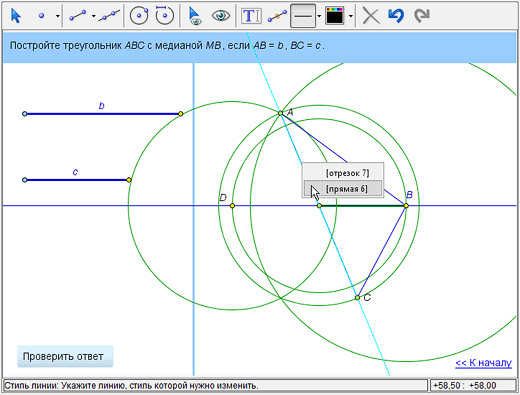
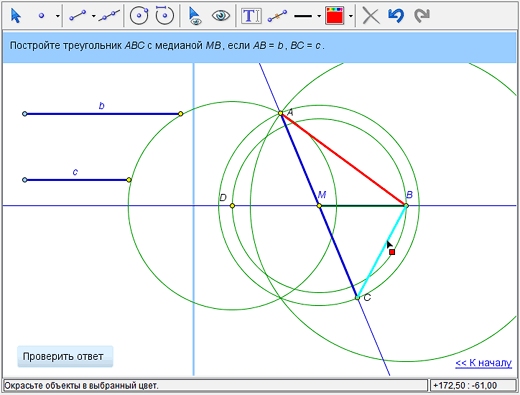
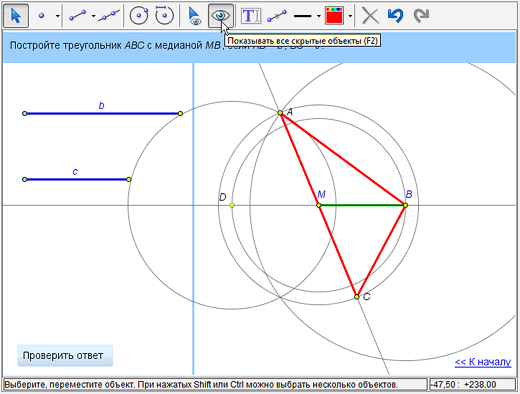
Во-вторых, можно скрыть вспомогательные линии, использованные при построении. Для этого выбираем инструмент «Скрыть/показать объект» и поочередно применяем его к окружностям, прямым, точкам – так, чтобы оставить видимыми только искомые отрезки АВ, ВС и СА. (Вы можете в любой момент «вернуть» спрятанные объекты – сделайте их временно видимыми при помощи кнопки «Показывать все скрытые объекты» и вновь воспользуйтесь инструментом «Скрыть/показать объекты» – на сей раз чтобы сделать объекты видимыми.)

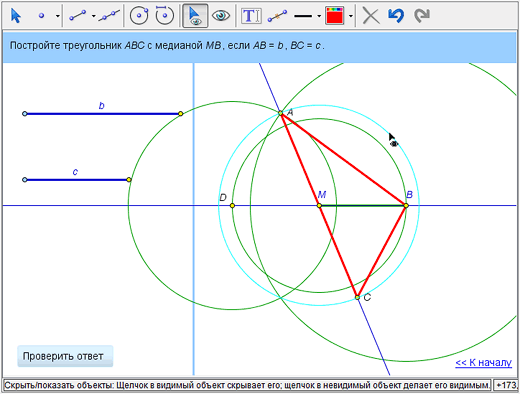
В-третьих, полезно отметить штрихами равные отрезки, на которые медиана делит отрезок АС. Для этого сначала нужно выбрать инструмент «Отметить отрезок штрихами» и указать концы отрезков АМ и МС (повторный выбор тех же отрезков добавляет штрихи в обозначение). Шрихи также можно покрасить.

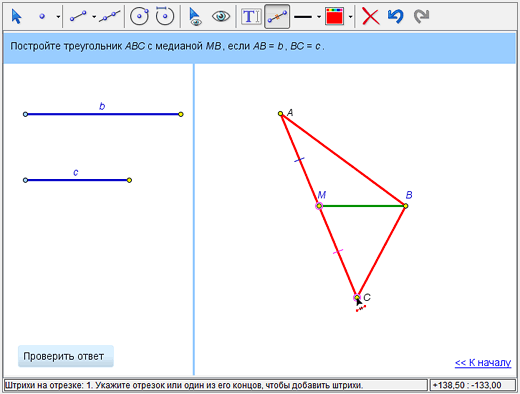
Осталось только насладиться динамическими возможностями правильного геометрического построения – меняя длины исходных отрезков, мы видим, как меняется и ответ, неизменно оставаясь правильным. Можно обнаружить и ситуации, когда построение искомого треугольника невозможно.

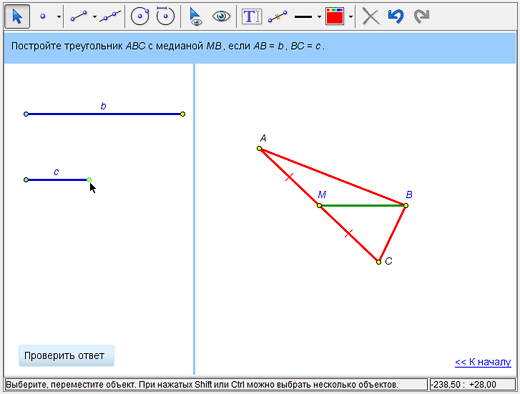
А как же вторая точка пересечения окружностей, рассмотренных на втором шаге построения? Можно было взять в качестве точки A и ее; тогда мы получили бы второй треугольник, симметричный построенному относительно BM. Обычно в таких случаях его не считают другим решением.