INTERACTIVE MODELS IN TEACHING AND LEARNING

Example: MathKit models after school

Around the Pythagorean Theorem

The Pythagorean theorem is the most famous theorem of geometry and, perhaps, of mathematics in general. Its wording is simple and visually clear:

The area of the square constructed on the hypotenuse of a right triangle
equals the sum of the areas of the squares constructed on its legs.

But it is far from being obvious. Because of these features or for other reasons, mathematicians take to proving it over and over again. In 1995, The Guinness Book of Records declared it the most proved theorem of all time. Let’s get to know some of them.

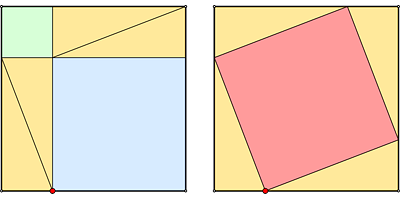
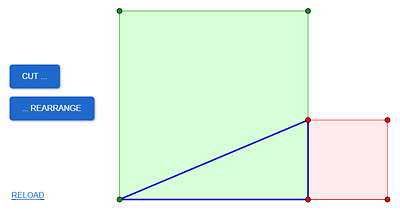
1. Pythagorean Proof

The proof of the Pythagorean theorem by dissection and rearrangement illustrated in this model is attributed to Pythagoras himself.

Model

It can also be used to derive the square of the sum formula.

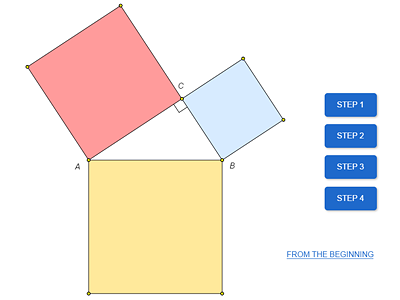
2. Euclidean Proof

A proof from Euclid’s Elements is illustrated in the following model.

Model

Explore the model and try to restore this proof.

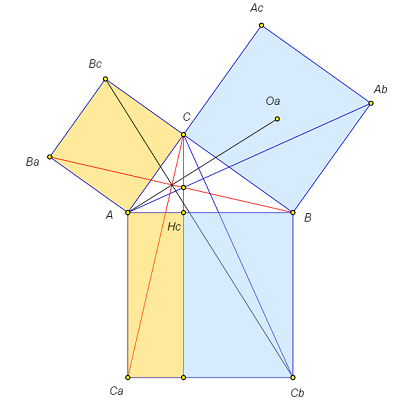
The construction used in this proof (see the figure) is variously called Bride’s chair, Peacock’s tail, Pythagorean pants (in Russia), and so on. This figure revealed a bunch of interesting properties that are not directly connected to the Pythagorean theorem. Investigation of these properties is suggested in Problem 2.

3. Behold!

Another ancient proof belongs to the great Indian mathematician of the 12th century Bhaskara. The proof is famous for a single-word explanation: Behold!

Model

4. The Hinged Proof

Rearranged pieces of the big square in Bhaskara’s proof form a combination of the two smaller squares placed side-by-side. This pentagonal shape is used in several different proofs of the Pythagorean theorem. The interesting thing about the argument known as the “hinged proof” is that here we cut this shape into the smallest possible number of pieces, just three, and rotate two of them, which are right triangles congruent to the initial one, around their vertices as hinges to obtain the square on the hypotenuse. Our animated model shows this rearrangement in action, while a strict proof is left to the reader.

Model

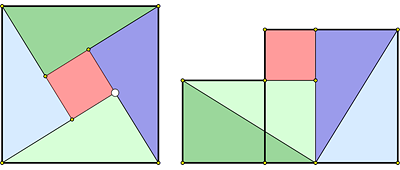
5. Pythagorean Tiling and Dissections

The two-square shape from the previous proof, shown in the middle of the figure below, tiles the plane. Of course, the same tiling can be viewed as composed of copies of the smaller squares from the Pythagorean theorem. This tiling yields a whole bunch of dissect-and-rearrange proofs. Perhaps, the most elegant of them, published by English amateur mathematician Henry Perigal in 1891, is obtained by considering the slanted square grid formed by the centers of the middle-sized squares.

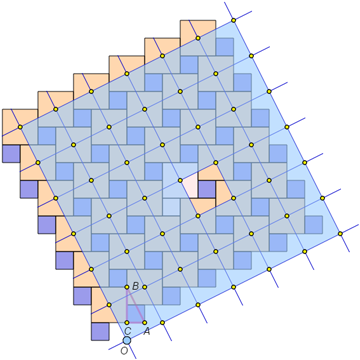Pythagorean tiling and "Perigal’s grid"

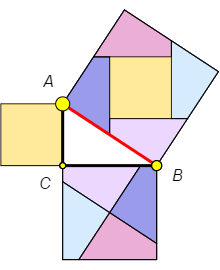Perigal’s proof

The side of each square of this grid is equal to the hypotenuse of the initial triangle (ABC in the figure at left). If we cut the plane along the lines of the grid and along the sides of the smaller squares from the tiling, then each grid square will be cut into five pieces: the smallest square and four congruent quadrilaterals. On the other hand, each middle-sized square is cut into the same four quadrilaterals. So the big square is the “sum” of the two smaller ones.

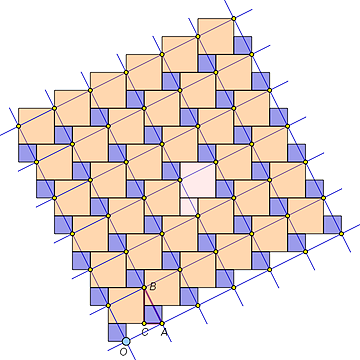How to obtain Al-Nayrizi’s proof from the Pythagorean tiling

Now imagine we shift the slanted grid over the tiling. Then we can repeat our argument for the new position of the grid and obtain infinitely many other dissection proofs with other pieces. One of these proofs, in which nodes of the grid are placed on the corners of the smallest squares, has been known from the works of a 9th-10th century Persian mathematician and astronomer Al-Nayrizi. This proof, as well as all the other tiling proofs are presented in the model of the Pythagorean tiling.

PROBLEMS

1. Constructions

Pythagorean theorem is used in various construction problems that involve calculations. Two of them are represented in these models:

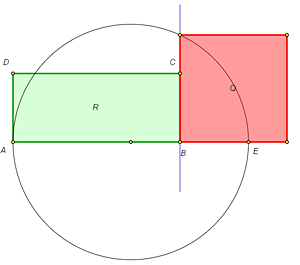Model

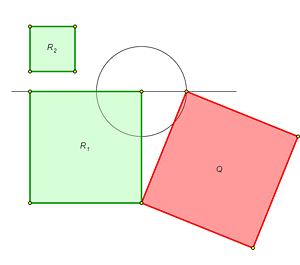Model

2. Bride’s Chair

Bride’s chair, the figure used in Euclid’s proof of the Pythagorean theorem, has been an object of close attention of generations of geometers for more than 2,000 years. No wonder it has revealed a bunch of interesting properties. For example, inspecting Euclid’s argument, we can notice that (a) the red segments in the figure below, as well as the blue ones, are congruent and perpendicular to each other. Not only that, the figure suggests that (b) the red and blue segments drawn from the endpoints of the hypotenuse meet on the altitude from the third vertex. Prove the properties stated above.

Model