INTERACTIVE MODELS IN TEACHING AND LEARNING

Example: MathKit model with guidelines

Partition into Two Equal Sums

Age	10-12
Subject	addition of natural numbers, comparison of natural numbers
Goals	to improve the skill of mental calculation; to consolidate the knowledge of order relations
How to use	under the teacher’s guidance or independently in a regular class or an after-school “mathematical circle.”

Description of the Model

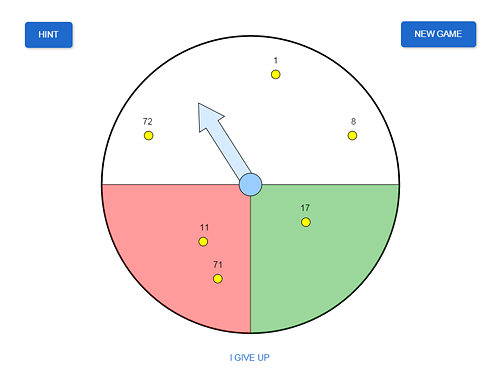
The model presents a conventional pan balance with two pans (the red and green sectors in the figure) and a hand. When you open the model or press the NEW GAME button, a set of “weights” (one- or two-digit numbers) is generated in the upper semicircle. You have to distribute all the weights on the pans so that the balance comes to the equilibrium (make the total weights equal). The numbers are always generated so that he problem has a solution, possibly non-unique. One solution can always be seen by clicking I GIVE UP.

The deviation of the hand from its central position is proportional to the difference between the weights on the pans. A correct solution is indicated by the upright position of the hand and the corresponding message. The HINT button displays the totals of the numbers on the pans. After a correct answer, the number of weights will increase, and the next question will be harder.

Model

Teacher Guidelines

This game can be used at any mathematics lesson to consolidate and develop the mental arithmetic skills. It can also be used at a mathematical circle and even a programming circle, with the aim of finding a winning strategy for the game and writing a program that realizes it.

1. Six numbers are given in the white semicircle. Students read the task. A discussion starts.

2. QUESTION: does the problem always have a solution?
   ANSWER: No, not always. Ask students to give an example of a set of six numbers for which the desired partition is impossible (e.g., 1,1,1,1,1,10).

3. QUESTION: can the problem have a solution if the number of weights is odd?
   ANSWER: yes, it can: the weights may not be equal (for instance, 1,1,2).

4. QUESTION: then what is a necessary condition for the problem to be solvable? What must be even?
   ANSWER: the sum of all the weights.

5. QUESTION: if the sum of the weights is even, does the problem necessarily have a solution?
   ANSWER: no (e.g., 1,1,10).

6. QUESTION: can the problem have several solutions, rather than one?
   ANSWER: yes, it can (e.g., 1,1,2,2,3,3).

7. Draw the students’ attention to the fact that by the design of the model, any problem it generates always has a solution, maybe not a single one. Now, finally, students can start playing by themselves.

8. After several solutions have been found (or the time allocated for the game has expired) you may want to discuss the strategies used by the children. These are some of possible options:

   • I placed the first number at random, but then always looked at the hand and dragged the next number on the pan with a smaller weight;
   • I followed a similar rule, but took into account not only the side on which the hand slanted, but also the magnitude of the difference, and tried to choose the next number as close to the difference as possible;
   • first, I added together all the numbers and divided the sum by 2 to write down the result: this was the sum that I had to collect in each sector. Then I tried to obtain this sum in the red sector; as soon as I succeeded, I moved the remaining weights to the green sector;
   • first I arranged the numbers in decreasing order; then I started to drag them on the balance one by one in this order, placing every number on a lighter pan;
   • my plan was the same as the previous one, but I retained the ordering on the pans as well; if I was unable to equalize the sums, it was easier for me to find a desired rearrangement of the weights
   and so on.

   All the strategies mentioned above are quite reasonable and can help us to find a solution, but none of them can guarantee that wе obtain an exact answer in the general case. They only are some heuristics, i.e. reasonable strategies that can speed up the search for a solution in many cases. The problem modeled here is known in informatics as the partition problem, or, in a slightly modified wording, as the backpack problem. It belongs to the class of NP-complete problems, i.e. the problems whose exact solution requires the complete search through all the possibilities.

   In this case a possibility is determined by the choice of a pan for each weight; the total number of such choices for 6 weights is 2⁶ = 64, and if we unite the symmetric distributions, it will only be 32; not much, indeed.

9. The game is repeated for new sets of numbers, which are generated by pressing the NEW GAME button. The number of weights in every new set grows by one until it reaches 15. After that only the values of the weights change. To make the problem more difficult, you can forbid the use of the hint.