MathKit 7

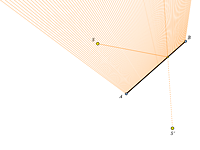
It is widely known that reflection of light rays is described by the law that briefly reads:
the angle of incidence is equal to the angle of reﬂection.

According to this law, a beam of light issued from a point S after reflection in a mirror segment AB forms a new beam of rays such that their extensions meet at a point S’, the reflection of S in AB. Such a point is said to be a virtual source of light.

Model 1

What happens for a curved mirror: a circle, parabola, or an even more complex curve? This question has been a matter of interest for physicists and mathematicians since antiquity.

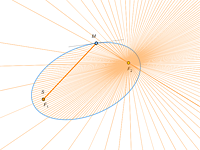
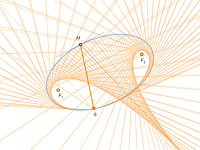
Source at the Focus

The optical properties of the ellipse, hyperbola, and parabola were known to ancient Greeks:

if a light beam is issued from a focus F₁ of an ellipse, then all its rays after reflection in the ellipse converge at the second focus F₂;

Model 2

if a light beam is issued from a focus F₁ of a hyperbola, then all its rays after reflection in the hyperbola diverge in such a way that their extensions meet at the second focus F₂;

Model 3

if a light beam is issued from a focus F of a parabola, then all its rays after reflection in the parabola form a beam of rays perpendicular to the directrix.

Model 4

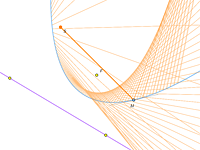
Moving the Source

The most interesting part of the show begins when we move the source of light off the focus.

Model 5

Model 6

Model 7

What you see in these models is called caustics (from the Greek kaustos, “burnt”). This is the surface (curve in the plane) near which the intensity of the light field formed by the reflected (or diffused) rays sharply grows. From the mathematical point of view, caustic is the envelope of the rays issued from a point (possibly infinite) and reflected from some curve.

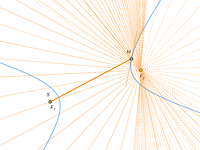
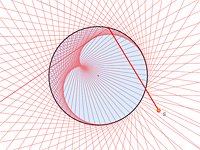
Caustic of a Circle

One caustic is certainly very well known to you. You can see it clearly every time you have your evening tea as a heart-shaped glowing trace on the cup’s surface.

Model 8

This is the cardioid, the envelope of rays reflected in a circle (of course, if the source of light is not in the center).

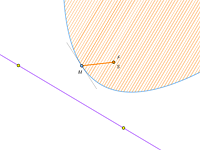
Caustics were studied not only by the Greek scientists: nowadays they became one of the central objects of interest for a relatively new area of mathematics, the catastrophe theory.

PROBLEMS

Problem 1 Given a straight line MN and points A and B on the same side of it, construct a point P on the line such that the length of the polyline APB is the smallest.

Problem 2 Given a straight line MN and points A and B on the same side of it, construct a point P on the line such that angles APM = 2 BPN.

Problem 3 Construct a model in which a circle is lit by a parallel beam of rays (the source is at infinity). To this end, model a “fluorescent tube,” i.e. a luminous line segment.

Problem 4 Try to derive the equation of a caustic. Prove that the caustic of a circle is

a cardioid if the rays radiate from a point;
a nephroid if the rays are parallel (source at infinity).

Check these results by constructing in MathKit the curves satisfying the equations you’ve obtained in MathKit.

Problem 5 Consider a refracted rather than reflected beam of light. Recall that Snell’s law of refraction of light crossing the boundary between two media (i.e. our curve) tells that for a given pair of media, n₁ • sin(θ₁) = n₂ • sin(θ₂), where n₁ and n₂ are the indices of refraction of the media and θ₁ and θ₂ are the angles of incidence and refraction (angles between the corresponding beams and the normal to the curve). Make a model of such a beam in MathKit and explore the caustics you obtain.

Problem 6 A ball starts moving on a round billiards table bouncing from its cushion. Prove that if the ball starts from a point other than the center, then it will never enter a certain circle on the table.

Problem 7 Alhazen’s Problem. A ball sits inside a round billiards table with one pocket. How to strike it so that after caroming off the cushion once it hits the pocket?

Problem 8 Consider Alhazen’s problem for an elliptic, parabolic, and hyperbolic billiards.