MathKit 7

MathKit, as a virtual lab, allows us to set up and conduct mathematical experiments. A well arranged experiment can lead to the discovery of an interesting mathematical fact. As a rule, such facts are visual; for example, we can discover experimentally that the medians or bisectors of a triangle are concurrent. Here we describe a guided discovery of a more advanced statement involving a formula, the classical Menelaus theorem.

We start with an extremely simple construction (much simpler than drawing medians) and an extremely simple action applied to it. Observation leads to conjectures, conjectures entail measurements, measurements produce plots, and plots suggest formulas, which, finally, can be checked by computations.

The accompanying model illustrates the steps of this discovery, which open up by pressing the buttons. However, it is mainly intended for a teacher. It would be best if students create this or similar model in the class from scratch, of course, under teacher’s guidance, which can be more or less detailed.

Setting up the Experiment

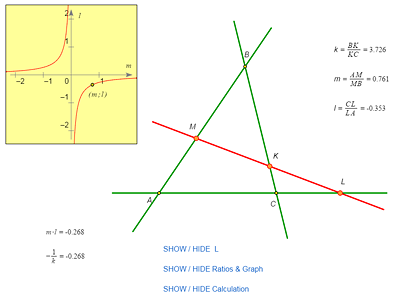
Construct a triangle ABC, take points M and K on its sides AB and BC, and draw the line MK. In view of what will follow, it’s recommended to draw the sides as (infinite) lines rather than segments and trim these lines.

Experiment and Observation

Let’s drag vertex B, without touching points A, C, M, and K, all over the plane.

Question: When you drag point B, what do you notice? Is there anything special in the behavior of the line MK?

Answer: The line always passes through a fixed point on the line AC.

Comment: To make this fact better visible, use the tracing of the line and construct the intersection point L of MK and AC.

Repeat the experiment for different positions of M and K.

Formalization

Our observation shows that the position of L is completely determined by the positions of M and K. Points M and K move together with B, but on the other hand, we see that they stay fixed with respect to the sides on which they are taken.

Question: How to specify the positions of points on the sides of a moving triangle?

Answer: by the ratios in which they divide the sides, k = BK/KC, m = AM/MB, and l = CL/LA.

As we've seen, one of them, l, is uniquely determined by the other two. Let’s measure them and use the measurements to find a formula that expresses the relationship between them.

Remark. MathKit’s Ratio tool gives signed ratios (the sign of, say, BK/KC depends on whether BK and KC, regarded as vectors have the same or opposite directions). Thus, originally, k and m are positive and l is negative, but as the points are dragged on their respective lines, the lines may change.

Processing the Data

Suppose that K (and therefore, k) is fixed. Then l is a function of m. We can create a coordinate frame and plot the graph of this function by plotting the point with coordinates (l; m) and constructing its locus as M sweeps the side line AB (this is why the sides of our triangle should better be lines rather than segments).

Question: What curve do you see and what, by virtue of your observation, is your assumption about the formula for this function?

Answer: This curve looks like a hyperbola. So we can try to assume that the product ml is a constant, which, naturally, depends on k.

Now we can check our assumption by computing ml: we see that, indeed, this product stays fixed as M moves.

Searching for the Final Formula

Denote the product ml, which depends only on k, by c(k). It would be great if we could find a formula for c(k), too. Then we’d have all the three ratios in one relationship. There are two ways to derive this formula.

Practical way. Drag K and compare the values of k and c(k) = ml. If you are keen enough, you may notice that they are inversely proportional. Otherwise, you can plot ml against k as we did above for l and m; you’ll obtain a hyperbola-like curve again, which allows us to surmise that k•c(k) is a constant.

Theoretical way. Alternately, we can notice without any additional constructions that the product of all the three ratios kml = k•c(k) depends (more exactly, can depend) only on k. But by the symmetry of our construction, it can just as well depend only on m. These means that kml is an absolute constant.

In any case, we come up with the conjecture that kml = const, which can be checked by calculations. Computing the product of the values k, m, and l, we find that it is equal to –1.

Conclusion

Thus, our observations allow us to conjecture the following theorem:

If a line meets the sides AB, BC, and CA of a triangle ABC or their extensions at points K, M, and L, respectively, then

This is the classical Menelaus theorem.

Of course, now it has to be proved, but this is a subject for another activity.