ТИПОЛОГИЯ УЧЕБНЫХ МОДЕЛЕЙ

1. Иллюстрации

Потребность сопроводить задачу иллюстрацией – одна из наиболее простых, но и наиболее часто возникающих на практике. В чем преимущество использования «Математического конструктора» для рисования таких иллюстраций? Сравним различные технологии построения чертежей.

• Чертеж в до-компьютерном понимании – это рисунок на бумаге или классной доске. Если делать его быстро – «от руки и на глаз», то страдает аккуратность, которая зачастую бывает существенна, точное же построение с помощью чертежных инструментов требует больших затрат времени. В любом случае такие иллюстрации трудно править, не переделывая заново.
  
  
• Рисование в растровых компьютерных графических редакторах (простейший из них – Paint). Точности достичь проще, но что-либо исправить в нем все равно трудно – придется стирать и рисовать заново.
  
  
• Рисование в векторных графических редакторах (такой редактор встроен в MS Word и MS PowerPoint; есть и многочисленные специализированные пакеты – CorelDraw, Adobe Illustrator и др.). Чертежи получаются качественные, все объекты легко редактируются. Однако векторные графические редакторы не обладают важнейшим свойством программ динамической геометрии – сохранением зависимостей между объектами.
  
  
• Чертеж, построенный в «Математическом конструкторе», принципиально отличается от чертежа, нарисованного в графическом редакторе. При изменении любого элемента такого чертежа сохраняются все заложенные в нем отношения: перпендикуляр к прямой останется перпендикуляром, биссектриса угла – биссектрисой, вписанная окружность – вписанной и т.д. Это свойство динамических чертежей открывает безграничный простор для разнообразных применений. О некоторых из них и идет речь ниже.
  
  

1.1. Рисуем сложный геометрический чертеж

В качестве первого примера рассмотрим иллюстрацию к теореме об окружности девяти точек. Построить этот, не столь уж простой чертеж с помощью коллекции макросов «Математического конструктора» – дело нескольких минут, и, что самое важное, при этом мы можем подобрать такую форму исходного треугольника, при которой четко видны все 9 рассматриваемых точек – такой чертеж можно вставлять в печатный документ.

Окружность 9-ти точек

Приведенная модель не только дает хороший чертеж, но и позволяет экспериментально убедиться в справедливости теоремы, варьируя треугольник, а также показывает построение по шагам и может быть использована на уроке.

Разумеется, при изучении геометрии не всегда нужно выполнять чертеж тщательно, доказательства можно проводить и при помощи эскизов, выполненных палочкой на песке. И все же удобный инструмент для создания аккуратных геометрических чертежей, которые порой способны подсказать ученику путь решения задачи, помешать не может.

1.2. Многовариантный чертеж: теорема Дезарга

Сам по себе чертеж к следующему примеру достаточно легко построить. Его особенность в другом – данные точки (вершины треугольников и центр перспективы O) можно произвольно перемещать, при этом конфигурация изменяется едва ли не до неузнаваемости. А для применения этой теоремы важно уметь ее увидеть в рассматриваемой фигуре. В книгах иногда помещают несколько вариантов расположения точек и прямых. Но все возможные случаи представлены в одной динамической модели. Наблюдать за ее преобразованиями весьма поучительно.

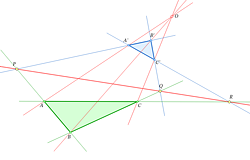Теорема Дезарга

Обратите внимание, что для большей ясности чертежа в нем использована возможность построения «укороченных» прямых, т.е. прямых, представленных отрезками длина которых динамически изменяется так, чтобы этот отрезок всегда содержал все построенные на прямой точки.

1.3. Строим графики функций аккуратно

Следующий пример иллюстрирует графическое решение уравнения

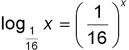
Интуиция в данном случае нас обманывает: если нарисовать графики левой и правой частей уравнения от руки, то мы «ясно увидим», что уравнение имеет один корень – на пересечении обоих графиков с прямой y = x (т.е. корень уравнения (1/16)^x = x). Но нетрудно заметить и проверить подстановкой, что числа x = 1/2 и x = 1/4 тоже являются корнями. Откуда же они берутся?

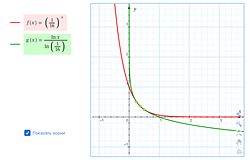Графическое решение уравнения

Если построить графики в «Математическом конструкторе», то программа найдет три точки их пересечения, хотя в окрестности этих точек при «нормальном» масштабе графики «слипаются». Пользуясь инструментом Изменить масштаб можно укрупнить изображение и увидеть, каким образом графики «переплетаются».

	ТИПОЛОГИЯ УЧЕБНЫХ МОДЕЛЕЙ