ИНТЕРАКТИВНЫЕ МОДЕЛИ В ОБУЧЕНИИ

Модель МК с методическими указаниями

Разбиение на две равные суммы

Возраст	10-12 лет
Тема	сложение натуральных чисел сравнение натуральных чисел
Цели	закрепление и развитие навыков устного счёта закрепление знаний об отношениях порядка
Как изучать	под руководством учителя или самостоятельно на уроке или кружке по математике

Описание модели

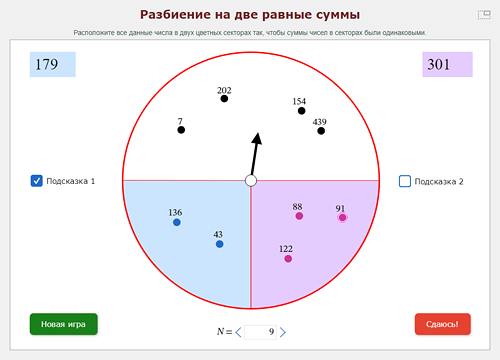
Имеется стилизованная модель весов в виде круга с двумя чашками (красный и зелёный секторы) и стрелкой. В верхнем секторе при открытии модели или по нажатию кнопки НОВАЯ ИГРА генерируется несколько однозначных или двузначных чисел-гирь. Требуется разложить все гири на две чашки весов так, чтобы суммы чисел на чашках были равными. Числа всегда задаются так, что задача имеет решение, возможно, не единственное. Одно из решений можно увидеть, нажав кнопку СДАЮСЬ!.

Отклонение стрелки весов от центрального положения пропорционально разности между двумя суммами. После правильного распределения всех чисел стрелка должна встать вертикально; при этом выводится сообщение об успешном решении. При нажатии на кнопку ПОДСКАЗКА на экране появляются подсказки в виде суммы чисел на каждой из чашек. По мере успешного решения задачи количество чисел будет увеличиваться.

Методические рекомендации

Игра может использоваться на любом уроке математики для закрепления и развития навыков устного счёта. Возможно использование игры на занятиях математических кружков, и даже кружка по программированию: в этом случае модель используется для поиска стратегии и последующего написания программы, решающей поставленную задачу.

1. В верхнем (белом) секторе 6 натуральных чисел. Ученики читают задание. Обсуждаем условия игры.

2. ВОПРОС: всегда ли задача имеет решение?
   ОТВЕТ: нет, не всегда. Попросите учащихся привести пример таких 6 чисел, когда это невозможно (например: 1,1,1,1,1,10).

3. ВОПРОС: для того, чтобы задача имела решение, обязательно ли количество чисел должно быть чётным?
   ОТВЕТ: нет, не обязательно – ведь числа могут быть разные (например: 1,1,2).

4. ВОПРОС: а какое условие должно обязательно выполняться, чтобы задача имела решение? Что должно быть чётным?
   ОТВЕТ: сумма чисел.

5. ВОПРОС: если сумма чисел чётна, это гарантирует, что задача имеет решение?
   ОТВЕТ: нет (например: 1,1,10).

6. ВОПРОС: может ли задача иметь не одно, а несколько решений?
   ОТВЕТ: да, может (например: 1,1,2,2,3,3).

7. Обратите внимание учащихся, что по условию игры для предложенных чисел задача всегда имеет решение (возможно, не одно). Теперь, наконец, можно предложить учащимся поискать ответ самостоятельно.

8. После того, как найдено несколько решений (или исчерпано отведённое для этого время) необходимо обсудить стратегии, которыми пользовались учащиеся. Возможны такие варианты:

   • я перетаскивал очередное число на одну из чашек и смотрел, куда отклонилась стрелка; следующее число прибавлял туда, где меньше;
   • я действовал похожим образом, но смотрел не только на стрелку, но и на величину разности; очередное число выбирал как можно ближе к этой разности;
   • сначала я сложил все числа и поделил сумму на 2, полученный результат S записал на бумаге – именно такая сумма должна получиться в каждом секторе; после этого пытался набрать сумму S в красном секторе; как только это получилось, отправил оставшиеся числа в зелёный;
   • сначала я упорядочил все числа по убыванию; после этого начал по порядку перетаскивать их на чашки, причём очередное число отправлял на ту чашку, где меньше;
   • я действовал так же, как в предыдущей стратегии, но на чашках тоже сохранял упорядоченность чисел: когда суммы всё-таки не сошлись, мне легче было найти варианты обмена чисел между чашками;
   и т.д.

   Все перечисленные стратегии вполне разумны и могут помочь в поиске решения, но ни одна из них в общем случае не гарантирует получение точного ответа. Это всего лишь эвристики, т.е. разумные стратегии, которые во многих случаях ускоряют поиск решения. Сама же задача известна в информатике как задача о разбиении или, в несколько изменённой формулировке, задача о рюкзаке. Задача относится к классу так называемых NP-полных задач, для точного решения которых требуется полный перебор всех вариантов.

   Здесь каждый вариант определяется выбором для каждого числа одной из двух чашек; всего таких вариантов для 6-ти чисел 2⁶ = 64, а если не рассматривать симметричные, то 32 – не так уж много).

9. Игра повторяется для новых наборов чисел, которые генерируются при нажатии кнопки НОВАЯ ИГРА. Количество чисел в каждом новом наборе увеличивается на 1, пока не достигнет 15. После этого меняются только значения чисел. Для усложнения задания можно запретить использование подсказки.