ИНТЕРАКТИВНЫЕ МОДЕЛИ В ОБУЧЕНИИ

МК и урок-открытие

Как совершить математическое открытие

«Математический конструктор» в роли виртуальной лаборатории позволяет ставить и проводить математические опыты. Хорошо поставленный эксперимент может привести к открытию интересных математических фактов. Обычно это какие-то наглядные, непосредственно наблюдаемые свойства; например, нетрудно обнаружить экспериментально, что медианы или биссектрисы треугольника пересекаются в одной точке. Здесь мы расскажем о том, как можно прийти к открытию менее очевидной теоремы, содержащей довольно сложную формулу, – классической теоремы Менелая.

Мы начнем с совсем простой конструкции (гораздо более простой, чем треугольник с медианами) и совсем простой ее трансформации. Наблюдение за ее поведением наталкивает на предположения, предположения влекут измерения, измерения порождают графики, а графики подсказывают формулы, которые, наконец, можно проверить вычислениями. Прилагаемая модель иллюстрирует шаги этого неблизкого пути, выполняемые по нажатию соответствующей кнопки. Отметим, что она адресована, прежде всего, учителю. Ученикам рекомендуется воспроизвести эту или похожую модель «с нуля» под более или менее пристальным присмотром учителя.

Постановка эксперимента

Построим треугольник ABC, возьмем точки M и K на его сторонах AB и BC и соединим их прямой MK. С учетом дальнейшего, рекомендуется изобразить стороны (бесконечными) прямыми, а не отрезками, а потом их «укоротить».

Эксперимент и наблюдение

Попробуем таскать вершину B по плоскости, не трогая точки A, C, M и K.

Вопрос: Что вы замечаете, перемещая точку B? Можно ли сказать что-то особенное о поведении прямой MK?

Ответ: Прямая проходит через постоянную точку на прямой AC.

Комментарий: Чтобы сделать этот факт более наглядным, используйте рисование следа прямой и постройте точку пересечения L прямых MK и AC.

Повторите опыт для разных положений точек M и K.

Формализация

Мы видим, что хотя при перемещении точки B точки M и K тоже движутся, их положения относительно сторон, на которых они лежат, остаются неизменными. Таким образом, наше наблюдение показывает, что положение точки L полностью определяется положениями точек M и K на соответствующих сторонах треугольника.

Вопрос: Как можно задать положения этих точек на сторонах изменяющегося треугольника?

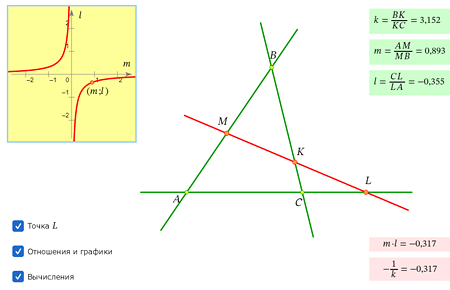
Ответ: отношениями, в которых они делят стороны: k = BK/KC, m = AM/MB и l = CL/LA.

Как мы видели, одно из них, а именно l, однозначно задается двумя другими. Давайте измерим эти отношения и используем результаты этих измерений, чтобы найти формулу, выражающую зависимость между этими отношениями.

Замечания. Инструмент Отношение изменяет отношения (со знаком) направленных отрезков (скажем, знак отношения BK/KC зависит от того, являются ли векторы BK и KC сонаправленными или противоположно направленными). Изначально k и m положительны, а l отрицательно, но если двигать точки по их прямым, знаки могут меняться.

Обработка данных

Временно фиксируем K (а значит, и k). Тогда l является функцией от m. Создадим систему координат и построим график этой функции, отметив в этой системе точку с координатами (l; m) и построив её геометрическое место, когда M пробегает прямую AB (именно для этого лучше в качестве сторон треугольника брать прямые, а не отрезки).

Вопрос: Какая у вас получилась кривая и какое можно высказать предположение о задающей ее формуле?

Ответ: Эта кривая похожа на гиперболу. Поэтому можно попробовать предположить, что произведение ml постоянно, но эта константа, естественно, зависит от k.

Теперь можно проверить наше предположение вычислением произведения ml: мы увидим, что при перемещении точки M оно действительно остается неизменным.

Поиск окончательной формулы

Обозначим произведение ml, которое зависит только от k, через c(k). Было бы здорово найти и формулу для c(k). Тогда мы получили бы зависимость сразу между всеми тремя отношениями. Приведем два способа вывода этой формулы.

Практический способ. Будем перемещать точку K и сравнивать величины k и c(k) = ml. Если вы достаточно наблюдательны, то сможете заметить, что они обратно пропорциональны. Можно также построить график зависимости ml от k, как это было сделано выше для l и m; снова получится кривая, похожая на гиперболу, что позволяет предположить постоянство произведения k•c(k).

Теоретический способ. Без всяких дополнительных построений можно заметить, что произведение kml = k•c(k) всех трех отношений зависит (точнее, может зависеть) только от k. Но в силу симметрии нашей конструкции, в которой точки K и M (а на самом деле, все три точки) играют одинаковую роль, это произведение может зависеть только от m. А это означает, что оно не зависит ни от k, ни от l, т.е. kml – абсолютная константа.

Так или иначе, мы приходим к предположению, что kml = const, которое можно проверить вычислением. Найдя произведение величин k, m и l, мы увидим, что оно равно –1.

Заключение

Итак, наши наблюдения позволяют предположить, что справедлива следующая теорема:

Если K, M и L соответственно – точки пересечения некоторой прямой со сторонами AB, BC и CA треугольника ABC или их продолжениями, то

Это классическая теорема Менелая.

Разумеется, ее еще нужно доказать, но это уже предмет для другого задания.