ИНТЕРАКТИВНЫЕ МОДЕЛИ В ОБУЧЕНИИ

Сценарий урока с использованием моделей МК

Классическое определение вероятности

Оборудование

• Проектор + ноутбук
• Компьютерный класс (для самостоятельного решения задач)

Цели урока

1. Знакомство с классическим определением вероятности.
2. Формирование умений в построении математических моделей случайных опытов.
3. Выработка навыков подсчёта вероятностей случайных событий в реальных ситуациях.
4. Дальнейшее развитие представлений о закономерностях, присущих случайным явлениям.

Структура урока

ЧАСТЬ 1

Сюжет 1

В этой части урока мы напомним, что такое статистическая вероятность и обсудим, можно ли её найти, не прибегая к опыту.

Цели сюжета

• напомнить учащимся о введённом ранее статистическом определении вероятности как предельном значения частоты;
• продемонстрировать с помощью компьютерного эксперимента процесс стабилизации частот с ростом числа опытов;
• поставить вопрос о возможности «предсказания» предельного значения частоты без проведения опыта.

Формы работы

• демонстрация модели с помощью проектора;
• коллективное обсуждение.

Возможный сценарий

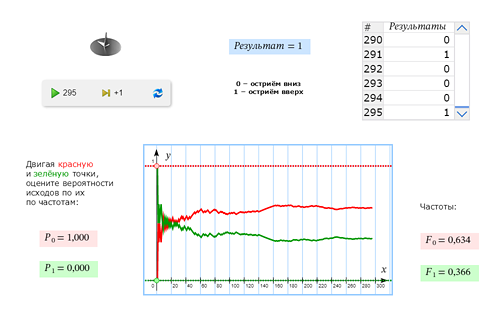
	Напомним, что вероятностью случайного события мы назвали число, около которого стабилизируется его частота при неограниченном увеличении количества опытов. Рассмотрим эксперимент с подбрасыванием канцелярской кнопки. Он может закончиться одним из двух исходов: кнопка может упасть на пол остриём вверх, или остриём вниз. Возьмётся ли кто-нибудь предсказать, чему равна вероятность каждого из них?
	Нет, для этого нужно провести опыты. Посмотреть, к каким числам будут приближаться частоты этих исходов.
	А можно ли сказать, чему равна сумма этих вероятностей?
	Да. Она равна 1.
	Давайте проведём опыт с кнопкой в нашей виртуальной лаборатории. Опыт с кнопкой Теперь вы можете хотя бы приближённо оценить эти вероятности?
	Да. Вероятности можно оценить по полученной частоте. Можно провести ещё больше опытов и получить более точную оценку.

Методические замечания.

При обсуждении данной модели можно сделать два важных замечания:

• вероятность заложена «в природе вещей»: если наш опыт с той же кнопкой повторить спустя неделю, частота будет стремиться к тому же числу (для кнопки, сделанной по другой технологии, это число может быть уже другим);
• значительные отклонения частоты от вероятности возможны даже при большом количестве опытов – но чем больше опытов, тем менее вероятны такие отклонения (вопрос об их количественных оценках выходит за рамки школьного курса).

Сюжет 2

Цель сюжета

• демонстрация простейшего опыта, в котором вероятности исходов можно предсказать без проведения опыта.

Формы работы

• демонстрация модели с помощью проектора;
• коллективное обсуждение.

Возможный сценарий

	В некоторых случаях можно «предсказать» вероятность (т.е. будущую частоту) без проведения эксперимента. Можете вы привести примеры таких опытов?
	Да: подбрасывание монеты, кубика, игра в рулетку и т.д.
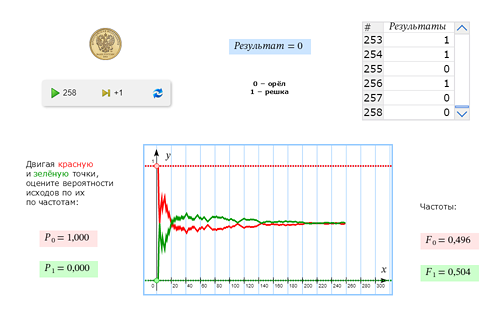
	Рассмотрим опыт с монетой. С какой вероятностью в этом опыте выпадет «орёл»?
	1/2
	Почему?
	Монета симметрична. У неё две стороны. Значит, у опыта два равновозможных исхода.
	Проверим этот ответ экспериментально. Опыт с монетой

Методические замечания

Возможно, кто-то из учащихся усомнится в симметрии монеты: ведь на одной её стороне выгравирован герб, а на другой цифра! И тем не менее, эти различия столь несущественны, что вполне удовлетворительной моделью реальной монеты может служить идеальная, для которой стороны равновозможны.

Сюжет 3

Цели сюжета

• демонстрация опыта с равновозможными исходами;
• подведение учащихся к классическому способу вычисления вероятности.

Формы работы

• демонстрация модели с помощью проектора;
• коллективное обсуждение.

Возможный сценарий

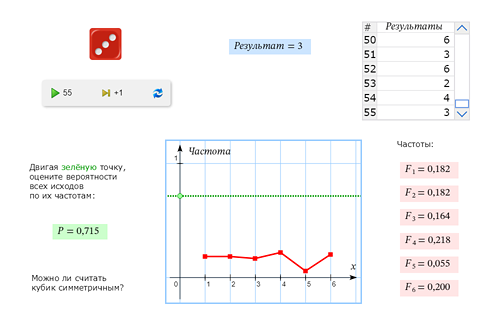
	Рассмотрим опыт с кубиком. С какой вероятностью на кубике выпадет 5 очков?
	1/6
	Почему?
	Кубик симметричен. У него 6 граней.
	Поставим эксперимент. Опыт с кубиком (Исходы) Изменяющийся график, который вы видите на экране, представляет собой так называемый полигон частот. По нему видно, как частоты всех шести исходов постепенно выравниваются по мере увеличения числа опытов.
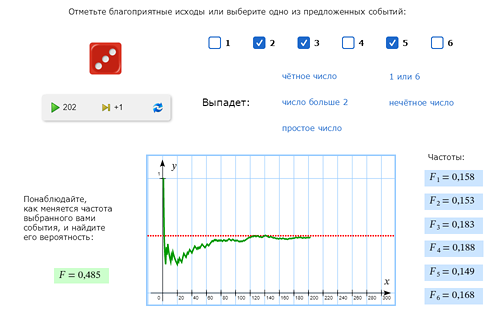
	А как найти в таком опыте с равновозможными исходами вероятности случайных событий, которые состоят уже не из одного, а из нескольких исходов? Попробуйте ответить на следующие вопросы: С какой вероятностью выпадет чётное число? Число, больше 2? Простое число? Объясните свои ответы. Каждый ответ мы проверим с помощью нашей модели. Опыт с кубиком (События)
	Правильные ответы: 1/2; 2/3; 1/2.

Методические замечания

При объяснении ответов учащиеся должны самостоятельно подойти к классическому определению вероятности, которое формулируется в следующем выводе.

Вывод

	В примерах с монетой и кубиком мы имели дело с симметричными предметами, поэтому все исходы опыта были равновозможными. При подбрасывании монеты было два равновозможных исхода – «орёл» и «решка», а при подбрасывании кубика – шесть (по числу его граней). В силу симметрии не было никаких оснований считать один из таких исходов вероятнее другого. В общем случае можно сформулировать следующее определение (оно называется классическим определением вероятности): Определение. Пусть случайный эксперимент может завершиться одним из n равновозможных исходов; и пусть ровно m из этих исходов благоприятствуют - т.е. приводят к наступлению - случайного события A. Тогда вероятность этого события может быть вычислена по формуле P(A) = m / n. Можно ли пользоваться этим определением в опыте с кнопкой?
	Нет, она не симметрична. Исходы не равновозможны.
	Чтобы воспользоваться этим определением, нужно определить все возможные исходы опыта; убедиться, что они равновозможны; вычислить n – число всех возможных исходов опыта; вычислить m - число исходов, благоприятных для заданного события A; найти P(A) = m / n.

Методические замечания

Обратите внимание учащихся на важность шага 2: если в нём сделана ошибка (выбраны не равновозможные исходы), то выполнение остальных пунктов бессмысленно.

ЧАСТЬ 2

На этом этапе урока только что сформулированное определение будет применено к вычислению вероятностей случайных событий в более сложных опытах.

Пример 1

Цели примера

• рассмотрение простейшего опыта, в котором элементарные исходы являются комбинациями;
• демонстрация равновозможности и неравновозможности исходов при различном их выборе.

Формы работы

• демонстрация модели с помощью проектора;
• коллективное обсуждение

Возможный сценарий

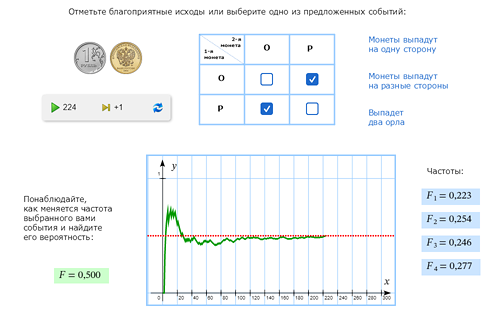
	Бросаем две монеты. Сколько равновозможных исходов у этого опыта? Перечислите их.
	Правильный ответ: 4 (ОО, ОР, РО, РР). Возможный неправильный ответ: 3 (два орла, две решки, орёл и решка).
	С какой вероятностью монеты выпадут на разные стороны? На одну сторону? Ответы объясните.
	Правильное решение: всего исходов – 4; благоприятных – 2 и 2; вероятности – 1/2 и 1/2. Неправильное решение: всего исходов – 3; благоприятных – 1 и 2; вероятности – 1/3 и 2/3.
	Проверим, кто прав, с помощью эксперимента: Две монеты Если считать, что опыт имеет 4 равновозможных исхода, изображённых на диаграмме, то для каждого из событий имеется по 2 благоприятных исхода, поэтому их вероятности будут по 1/2. Это подтверждается поведением частот.

Методические замечания

Если при подсчёте числа исходов все ученики единогласно ответят 4, то учитель сам может принять неправильную точку зрения и привести в доказательство 3 исхода (так называемая «ошибка Даламбера», которую тот сделал в одном из своих рассуждений о вероятности).

Пример 2

Цели примера

• рассмотрение опыта, в котором элементарные исходы являются парами чисел;
• демонстрация наглядного способа подсчёта благоприятных исходов с помощью таблицы.

Формы работы

• демонстрация модели с помощью проектора;
• коллективное обсуждение;
• работа у доски.

Возможный сценарий

	Бросаем два кубика. Сколько равновозможных исходов у этого опыта? Что они собой представляют?
	36 исходов. Это все возможные пары чисел из диапазона от 1 до 6.
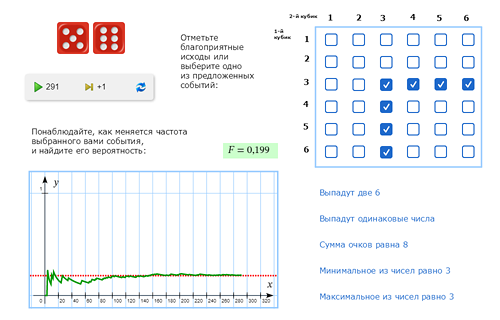
	Такие пары можно представить в виде клеток таблицы 6x6, приведённой в модели. Найдём с её помощью все благоприятные исходы для каждого из следующих событий: A = {выпадут две 6}, B = {выпадут одинаковые числа}, C = {сумма очков будет равна 8}, D = {максимальное из чисел будет равно 3}, E = {минимальное из чисел будет равно 3}. Два кубика (Исходы и События)
	Кто-то из учеников выходит к доске и пробует ответить на поставленные вопросы с помощью модели. Правильные ответы: 1; 6; 5; 5; 7.
	Теперь несложно будет найти вероятности каждого и перечисленных событий.
	Ответы: 1/36; 1/6; 5/36; 5/36; 7/36;
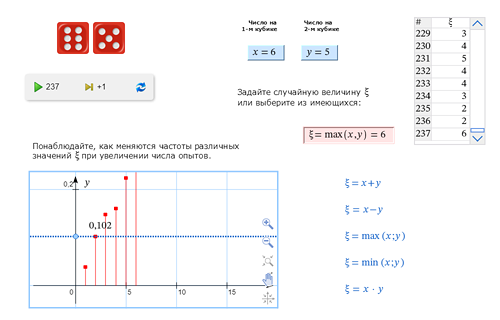
	А теперь, используя ту же модель, попробуем ответить на такие вопросы: Какое значение суммы наиболее вероятно? Какое значение разности наиболее вероятно? Какое значение минимума наиболее вероятно? Какое значение максимума наиболее вероятно? Какое значение произведения наиболее вероятно? Для проверки ваших ответов используем ту же модель: Два кубика (Случайные величины)
	Кто-то из учеников выходит к доске и пробует ответить на поставленные вопросы с помощью модели. Все полученные ответы проверяются экспериментально. Правильные ответы: 7; 0; 1; 6; 6 и 12.

Методические замечания

Пример служит хорошей пропедевтикой понятия случайной величины – центрального понятия второй половины курса теории вероятностей. По-существу в последнем задании изучаются законы распределения случайных величин Sum, Diff, Min, Max, Prod.

Пример 3

Цели примера

• рассмотрение сложного опыта, в котором впервые появляется схема последовательного выбора без возвращения (или одновременного выбора) на примере выбора двух шаров из урны;
• обсуждение свойства "элементарности" исходов, как одного из условий их равновозможности.

Формы работы

• демонстрация модели с помощью проектора;
• коллективное обсуждение.

Возможный сценарий

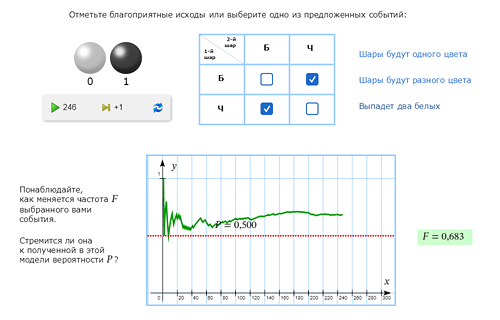
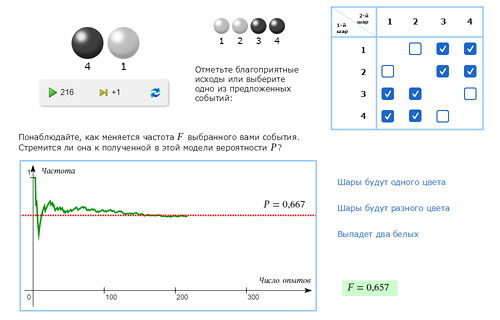
	Из урны, в которой 2 белых и 2 чёрных шара, наугад вытаскивают 2 шара. С какой вероятностью они будут разного цвета?
	Возможные неправильные ответы: 1/2, 1/4, 1/3. Правильный ответ – 2/3 – даётся, как правило, реже всего.
	Начнём с ответа 1/2. Очевидно те, кто его предложили, имели в виду следующую модель, уже знакомую нам по опыту с двумя монетами: Два белых и два чёрных шара (Ошибочная модель) Но в данном опыте такая модель не работает! Чтобы убедиться в этом, запустим серию экспериментов. Видим, что выбранные 4 исхода неравновозможны. Как вы думаете, почему исходы ББ и ЧЧ выпадают гораздо реже?
	???
	Объяснение может быть такое: выбранные исходы НЕ элементарны, а поэтому и НЕ равновозможны. Природа различает шары, а не их цвета. Представьте, что в урне 2 белых и 2 млн. чёрных шаров. Теперь неравновозможность исходов становится очевидной. Каким исходом почти наверняка завершится наш опыт?
	Конечно, ЧЧ.
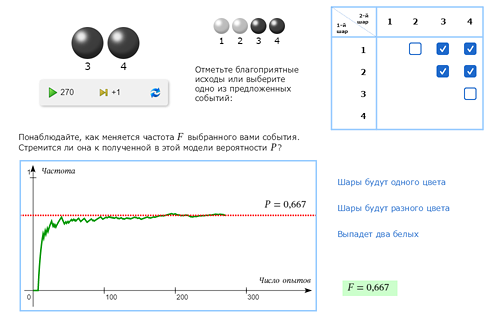
	А теперь посмотрим, как выглядит правильная модель. Два белых и два чёрных шара (Правильная модель) Если пронумеровать все шары, и вытаскивать их один за другим, то опыт, как видно из таблицы, будет иметь (16-4)=12 равновозможных исходов (исключаются 4 пары с одинаковыми числами). Будем считать, что шары 1 и 2 – чёрного цвета, а 3 и 4 – белого. Тогда нетрудно выделить все благоприятные для нашего события исходы и убедиться, что их 8. Ответ: вероятность, что шары будут разного цвета равна 8/12 = 2/3.
	Тот же ответ можно получить гораздо быстрее таким простым рассуждением: вытащим первый шар. Какого бы он ни был цвета, в ящике осталось 3 шара, из которых только один имеет тот же самый цвет, и два шара – другой цвет. Значит, вероятность вытащить на втором шаге шар НЕ ТОГО ЦВЕТА, ЧТО УЖЕ ВЫТАЩЕН, равна 2/3. Этот способ также можно проиллюстрировать с помощью модели: Два белых и два чёрных шара (Другая модель)

Методические замечания

1. Если на вопрос задачи будет сразу предложен правильный ответ – 2/3 – и других не будет, то роль «незнайки» может взять на себя учитель; при этом объяснение неправильных ответов может быть, например, таким:

   • 1/2 – нужно взять систему исходов {ББ, БЧ, ЧБ, ЧЧ};
   • 1/3 – система исходов {ББ, БЧ, ЧЧ} (здесь БЧ и ЧБ не различаются, поскольку шары извлекаются одновременно).

2. При построении «правильной» модели можно не учитывать порядок вытаскивания шаров (т.е. шары вытаскивают одновременно) и тогда равновозможных исходов будет не 12, а 6. Но и количество благоприятных также уменьшится вдвое, поэтому правильный ответ сохранится – 4/6 = 2/3.

Игра

Цели игры

• демонстрация практической ценности классического определения вероятности при оценке шансов в игре;
• обсуждение одного из важнейших отношений в математике – отношения транзитивности.

Формы работы

• проведение игры с классом с использованием компьютерной модели;
• коллективное обсуждение результатов.

Возможный сценарий

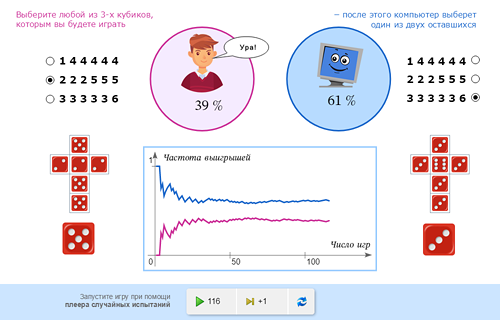
	Имеются три необычных (но «правильных») кубика, на гранях которых написаны следующие числа: кубик A: 1,4,4,4,4,4 кубик B: 2,2,2,5,5,5 кубик C: 3,3,3,3,3,6 Вы можете выбрать любой из кубиков. После этого я выбираю один из оставшихся и мы играем в «подбрасывание кубиков»: если на вашем кубике число больше, чем на моём, то вы выиграли и наоборот. Какой кубик вы выбираете?
	Возможные ответы: A (B, C).
	Тогда я выбираю (соответственно) B (C, A). После одной или даже нескольких игр «сила» того или другого кубика вряд ли проявится, поэтому проведём сразу целую серию игр и определим , кто же будет выигрывать чаще. Игра “Три кубика” Ученикам предлагается сменить свой выбор. Они снова проигрывают. Наконец, последняя, третья попытка – и опять неудача.
	Разберёмся, почему же второй игрок всегда выигрывает чаще – ведь у первого преимущество в выборе «сильнейшего» кубика. Оказывается, если сравнивать кубики в парах, среди них нет абсолютно лучшего. Вспомните детскую игру «Камень-Ножницы-Бумага»: камень затупляет ножницы, ножницы режут бумагу, а бумага оборачивает камень. Давайте, используя классическое определение вероятности и компьютерную модель игры, вычислим и сравним между собой вероятности каждого из следующих событий: P(B>A) и P(A>B), P(C>B) и P(B>C), P(A>C) и P(C>A).
	Кто-то из учеников выходит к доске и с помощью класса и компьютерной модели находит благоприятные исходы, подсчитывает их количество и вычисляет вероятности: P(B>A) = 21/36 и P(A>B) = 15/36, P(C>B) = 21/36 и P(B>C) = 15/36, P(A>C) = 25/36 и P(C>A) = 11/36.
	Итак, в парных играх B лучше A, C лучше B, A лучше C. Значит, лучше выбирать кубик вторым, когда известен выбор первого игрока. А если мы будем играть втроём, то как вы будете действовать? Подумайте над этой задачей дома. Мы обсудим ваши ответы и проведём компьютерный эксперимент.

Методические замечания

1. Выявленный парадокс носит название парадокса нетранзитивности. Суть его в том, что отношения, которые в обычной жизни обозначаются словами «больше», «лучше», «сильнее» и т.д. воспринимаются обычно, как транзитивные: если A лучше В, а B лучше C, то A лучше C. Однако, это далеко не всегда так: скажем, отношение «больше» для чисел этим свойством обладает, а отношение «сильнее» для шахматистов по итогам личных встреч уже нет.

2. Ответ на последний вопрос звучит так: надо выбирать первым и взять кубик B. Вероятность, что максимально из трёх чисел окажется на кубике A равна 75/216 , на кубике B – 90/216, на кубике C – 51/216.

ЧАСТЬ 3

Задачи

Задача 1 (a)	(a) У маленькой Вари две одинаковые пары варежек. Уходя на улицу, она наугад берет две варежки. Какова вероятность того, что они окажутся парными (т. е. на разные руки: одна левая, другая - правая)?
Задача 1 (b)	(b) В предыдущей задаче (a) Варя потеряла одну варежку. Она снова собирается на прогулку и выбирает две варежки теперь уже из трёх. Вопрос всё тот же: с какой вероятностью они окажутся парными?
Задача 2	10 человек делятся по жребию на 2 равных команды. С какой вероятностью Петя и Вася будут играть в разных командах? В одной команде?
Задача 3	3 человека пришли в ресторан в одинаковых шляпах и сдали их в гардероб. Расходясь, они надели их наугад. С какой вероятностью каждый уйдёт в своей шляпе? В чужой шляпе?
Задача 4	Номер автомобиля состоит из 3-х цифр. С какой вероятностью случайно выбранный номер будет симметричным?
Задача 5	Найдите вероятность того, что снова получится то же самое слово, если перемешать и выложить в ряд буквы слова (a) МЫЛО; (b) РАМА; (c) МАМА.
Задача 6	В шкафу находятся 4 пары ботинок с 42-го по 45-й размеры. Из них случайно выбирают два ботинка. С какой вероятностью они окажутся парными (т.е. одного размера)?
Задача 7	В шкафу находятся 4 одинаковые пары ботинок 45-го размера. Из них случайно выбирают два ботинка. С какой вероятностью они окажутся парными (т.е. на разные ноги)?
Задача 8	В группе туристов 5 человек. С помощью жребия они выбирают двух человек, которые должны идти в село за продуктами. Паше не хочется идти в магазин, но он подчиняется жребию. Какова вероятность того, что Павел пойдёт в магазин?
Задача 9	Из Наташиного класса, в котором учатся 6 мальчиков и 9 девочек, по жребию выбирают двух дежурных. Какова вероятность, что (a) Наташа будет дежурить? (b) дежурить будет Наташа и ее подруга Света? (c) дежурить будут мальчик и девочка?