ИНТЕРАКТИВНЫЕ МОДЕЛИ В ОБУЧЕНИИ

МК в проектной деятельности

Каустики

Все знают закон отражения световых лучей, который коротко формулируется так:
угол падения равен углу отражения..

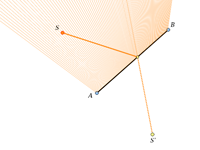
Согласно этому закону, пучок света, выпущенный из точки S, после отражения от «зеркального» отрезка AB, образует новый пучок лучей, продолжения которых пересекаются в точке S’ – образе точки S при осевой симметрии относительно AB. Это так называемый мнимый источник света.

Модель 1

А что получится, если искривить «зеркало» – сделать его окружностью, параболой или какой-нибудь более сложной кривой? Ответ на этот вопрос давно интересовал математиков и физиков.

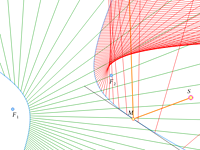
Источник в фокусе

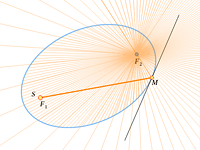
Еще в Древней Греции были известны оптические свойства эллипса, гиперболы и параболы:

если выпустить пучок света из фокуса эллипса F1, то все лучи, отразившись от эллипса, соберутся в фокусе F2;

Модель 2-1

если выпустить пучок света из фокуса гиперболы F1, то все лучи, отразившись от гиперболы, разойдутся так, что их продолжения пересекутся в фокусе F2;

Модель 3-1

если выпустить пучок света из фокуса параболы F, то все лучи, отразившись от параболы, образуют пучок, параллельный оси параболы.

Модель 4-1

Смещаем источник

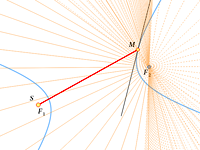
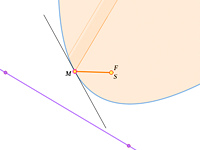
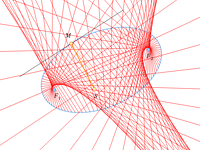
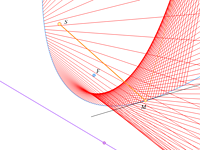
Самое интересное начинается, если мы сместим источник света и расположим его не в фокусе.

Модель 2-2

Модель 3-2

Модель 4-2

То, что вы видите в этих моделях, называется каустикой (от греческого kaustikos – жгучий, палящий). Это поверхность (на плоскости – кривая), в окрестности которой резко возрастает интенсивность светового поля, образованного отражёнными (или рассеянными) лучами. С точки зрения математики, каустика – это огибающая семейства лучей, выпущенных из одной точки (м.б. бесконечно удалённой) и отражённых от какой-либо кривой.

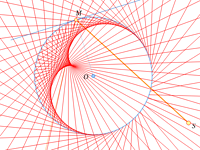
Каустика окружности

Одна из каустик вам хорошо знакома: если заглянуть во время вечернего чаепития в чашку, то на её поверхности хорошо виден светящийся след в форме «сердечка».

Модель 5

Это кардиоида – огибающая семейства лучей, отражённых от окружности (если, конечно, источник света находится не в её центре).

Каустики интересовали не только древнегреческих учёных: в наше время они стали одним из центральных объектов изучения в новой области математики – теории катастроф.

ЗАДАЧИ

Задача 1	Дана прямая MN и точки A и B, по одну сторону от неё. Постройте на прямой такую точку P, чтобы длина ломаной APB была минимальной.
Задача 2	Дана прямая MN и точки A и B, по одну сторону от неё. Постройте на прямой точку P так, чтобы ∠APM = 2 ∠BPN.
Задача 3	Постройте модель, в которой окружность освещается параллельным пучком света (источник находится на бесконечности). Для этого смоделируйте светящийся отрезок – «лампу дневного света».
Задача 4	Попробуйте вывести уравнение каустики. Докажите, что каустикой окружности будет кардиоида, если лучи выходят из точки; нефроида, если лучи параллельны (источник на бесконечности). Убедитесь в этом, построив в MK кривые, удовлетворяющие полученным уравнениям.
Задача 5	Рассмотрите не отражённый, а преломлённый пучок света. Напомним, что закон преломления света при прохождении через границу двух сред (т.е. через нашу кривую) выглядит так: n1 • sin(θ1) = n2 • sin(θ2), где n1 и n2 - показатели преломления среды, а θ1 and θ2 - углы падения и преломления. Смоделируйте такой пучок в МК и изучите, какие каустики получаются.
Задача 6	Из произвольной точки круглого бильярдного стола пущен шар. Докажите, что внутри стола найдётся такая окружность, что траектория шара её ни разу не пересечёт.
Задача 7	Задача Альхазена. Внутри круглого бильярдного стола с одной лузой лежит шар. Нужно послать его дуплетом (т.е. отражением от бортика) в лузу.
Задача 8	Рассмотрите задачу Альхазена для оптического, параболического, гиперболического бильярдов.