ИНТЕРАКТИВНЫЕ МОДЕЛИ В ОБУЧЕНИИ

Занимательная математика с моделями МК

Вокруг теоремы Пифагора

Теорема Пифагора – самая известная теорема геометрии, да пожалуй, и всей математики. Она проста и наглядна по своей формулировке:

Площадь квадрата, построенного на гипотенузе прямоугольного треугольника,
равна сумме площадей квадратов, построенных на катетах.

Но она отнюдь не очевидна. Наверное, эти качества и побудили математиков доказывать её вновь и вновь. В результате она попала в «Книгу рекордов Гиннеса», как теорема, получившая наибольшее число доказательств. Познакомимся с некоторыми из них.

1. Доказательство Пифагора

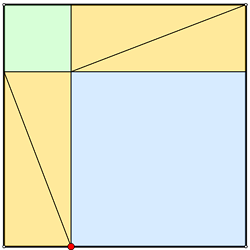
Доказательство теоремы Пифагора, использующее два разрезания квадрата и сравнение частей, которое иллюстрирует эта модель, приписывается самому Пифагору.

С его помощью можно также вывести алгебраическую формулу для квадрата суммы.

2. Доказательство Евклида

Доказательство теоремы Пифагора, данное Евклидом в его «Началах», приводится в следующей модели:

Исследуйте ее и попробуйте восстановить это доказательство.

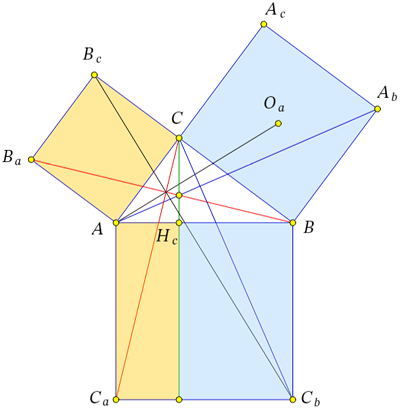
Конструкция, использованная в этом доказательстве (см. рисунок), в России называется «Пифагоровы штаны», а в других странах – «кресло невесты», «хвост павлина» и т.д. В этой фигуре обнаружился целый ряд интересных свойств, непосредственно не связанных с теоремой Пифагора; приведенная ниже Задача 2 посвящена исследованию этих свойств.

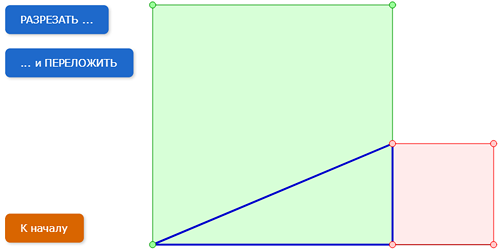
3. Смотри!

Другое старинное доказательство принадлежит великому индийскому математику 12-го века Бхаскаре Ачариа. Это доказательство прославилось тем, что автор пояснил его только одним словом: «Смотри!».

4. Шарнирное доказательство

Пятиугольная фигурка из предыдущего доказательства, составленная из двух квадратов со сторонами, равными катетам данного прямоугольного треугольника, встречается в нескольких разных доказательствах теоремы Пифагора. Так называемое «шарнирное доказательство» замечательно тем, что в нем эта фигура разрезается на наименьшее возможное число частей – три. Затем две из них – треугольники, равные данному, поворачиваются вокруг одной из своих вершин как шарнира в новое положение. В результате получается квадрат, сторона которого равна гипотенузе. Модель показывает, как это происходит, а строгое доказательство предлагаем провести самостоятельно.

5. Пифагорово замощение и разрезания

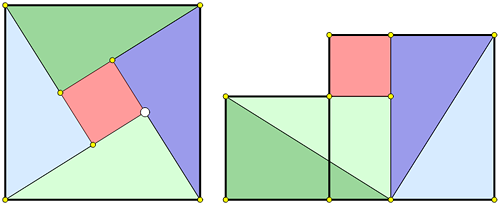
С помощью той же пятиугольной фигуры из двух квадратов можно замостить плоскость (это замощение показано на рисунке внизу слева; одна пятиугольная «плитка» выделена). Можно считать, что это замощение составлено из копий двух меньших квадратов из теоремы Пифагора. Оно порождает бесконечное множество доказательств, использующих равносоставленность. Для этого нужно наложить на наше замощение наклонную решетку из квадратов со стороной, равной гипотенузе исходного треугольника (треугольника ABC на рисунке слева). Одно из расположений решетки показано на рисунке; здесь каждая вершина наклонного квадрата является общей вершиной двух меньших квадратов. Линии решетки разрезают меньшие квадраты на кусочки, и нетрудно увидеть, что из кусочков, попадающих в один большой квадрат, можно составить оба малых квадрата, а значит, площадь большого квадрата равна сумме площадей малых квадратов. Указанный способ разрезания приводится в работах персидского математика и астронома IX–X веков Ал-Найризи.

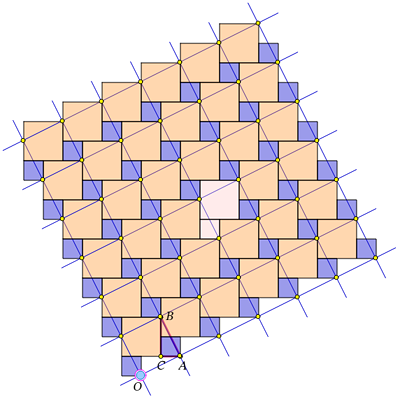
Пифагорово замощение

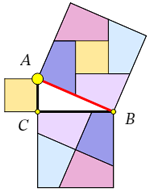
Доказательство Перигэла

Теперь будем двигать наклонную решетку по нашему замощению. Тогда каждое новое ее положение порождает новый способ разрезания квадратов, при котором большой квадрат и оба малых можно составить из одного и того же набора кусочков. И каждое новое разрезание дает новое доказательство теоремы Пифагора. Наиболее красивое из них было опубликовано английским математиком-любителем Генри Перигэлом в 1891 г. (см. рисунок справа). В этом доказательстве большой квадрат разрезается всего на пять кусков; один из равен самому маленькому квадрату, четыре других – равные четырёхугольники, из которых составляется «средний» по размеру квадрат. Этот способ разрезания мы получим, если поместим вершины наклонной решетки в центры «средних» квадратов.

ЗАДАЧИ

1. Построения

Теорема Пифагора используется во многих задачах на построение методом вычислений. Две такие задачи представлены в следующих моделях:

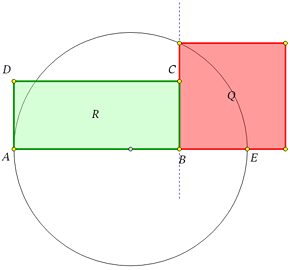
Задача 1

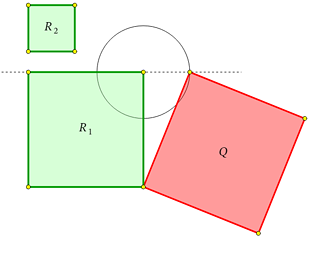
Задача 2

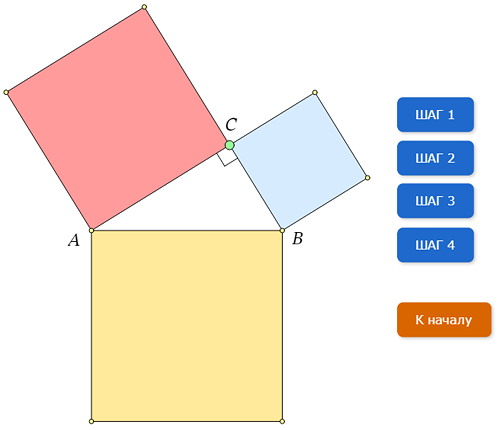
2. «Пифагоровы штаны»

Фигура, использованная в евклидовом доказательстве теоремы Пифагора, была объектом изучения геометров на протяжении более, чем 2000 лет. Неудивительно, что у нее обнаружился целый ряд интересных свойств. Например, анализируя евклидово доказательство, можно заметить, что (а) красные отрезки на рисунке внизу, так же как и синие, равны и перпендикулярны друг другу. Более того, как видно из картинки, (б) красный и синий отрезки, проведенные из концов гипотенузы, пересекаются на высоте треугольника, проведенной из третьей вершины. Докажите эти свойства.